Meshing is used in computational solving. It is a representation of the geometry that is involved in the problem, whether that be external or internal flow, or mechanical stress analysis, or heat rejection, or radio waves. Computer programs have been designed to analyze nearly any and every real-world situation, for good reason! Meshing is extremely important to accuracy, and ANSYS’s meshing capabilities are at the top of the field.

When and where do we use mesh?
Anytime a computational analysis needs to be performed, we must use mesh. Mesh allows complex shapes to be boiled down to simple shapes that a computer can solve. This means, for Verus, FEA, and CFD. Each and every analysis we do requires a component or environment to
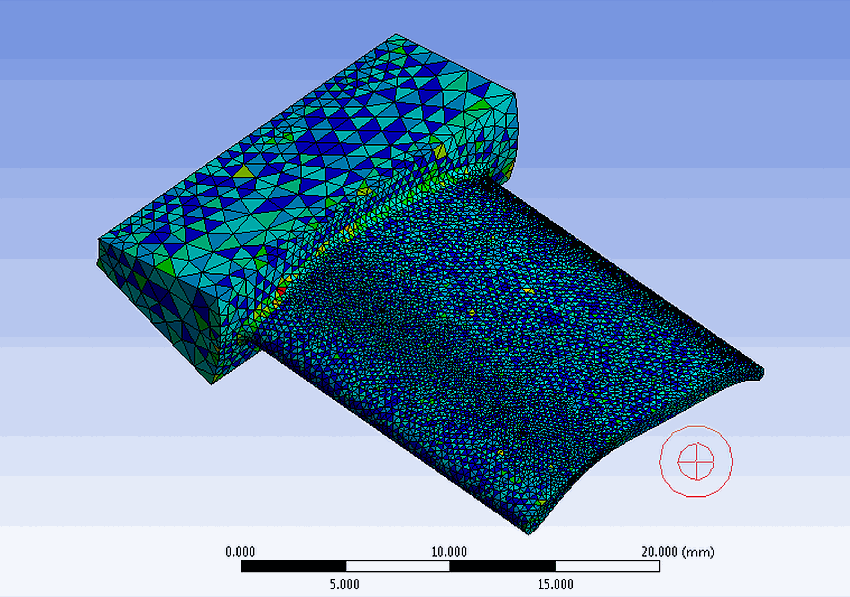
What does mesh look like?
Below are a few photos representing a typical mesh. While it appears that mesh is only on the surface, this is not the case. Mesh represents the entire solid of the body of the case study.
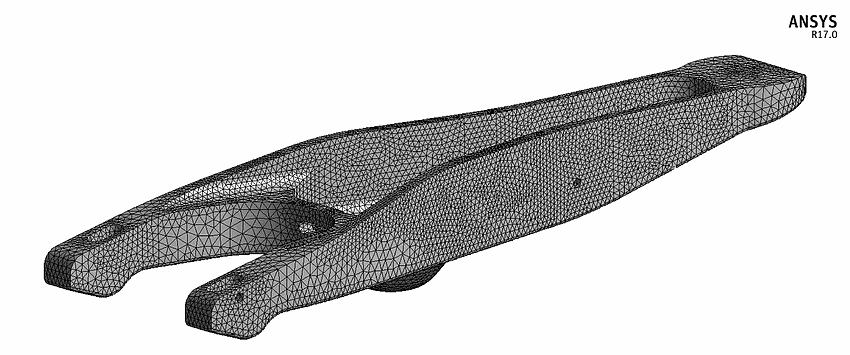
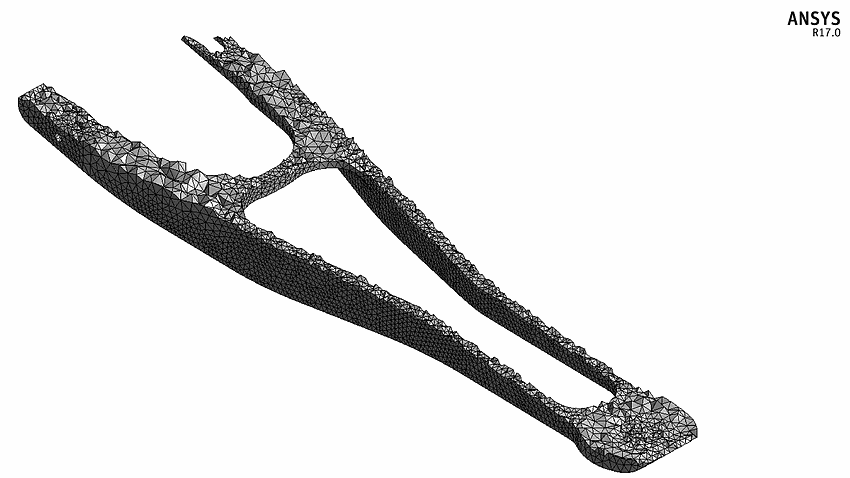

Why is meshing necessary?
Computers cannot solve the actual geometry’s shape as the governing equations cannot be solved for them. Enter meshing. Meshing creates a set of grid points called “nodes,” which is representative of the actual geometry. These elements allow governing equations to be solved which were not able to be solved previously! Typically these equations are partial differential equations, which are not easy to handle by hand calculations. This is why computationally is typically superior for abnormal shapes, though hand calculations can be used for simple shapes. Typically, the finer the mesh the more accurate the analysis. However, this is a balancing act as computation time and workload increases significantly with mesh density.
TLDR: Meshing is necessary to solve partial differential equations in computational analysis.
What styles of
Triangles and quadrilaterals are used in the
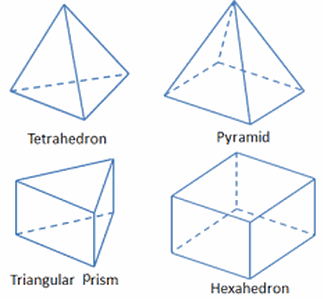
What goes on in the mesh?
Relevant governing equations, typically partial differential equations, are solved. This means tens to multiple hundreds of thousands of equations are solved for each iteration for FEA typically, and 3-20 million equations every iteration for our CFD analysis.
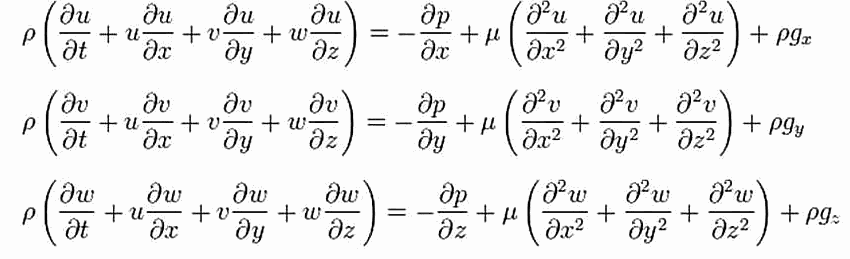
What are the consequences of a poor mesh?
Inaccurate results and solutions would be the main concern. Without a good mesh, it would be irresponsible to
expect accurate results. With CFD, a poor mesh will not converge. Without convergence, the solution is never reached.
We hope this helps clear up some questions regarding mesh and the necessity for its use. If you have further questions, please don't hesitate to ask.
Meshing – All You Need To Know