When developing aerodynamic components, placement matters. We will prove this point by placing a wing at various heights from the ground and observing the data. Would you be able to guess the height off the ground this wing would make peak downforce? What about peak efficiency?
We will be viewing CFD images of 4 heights off the ground. However, we ran 30 iterations at a change in distance of 5mm starting at 5mm from the ground. The 4 heights we outline below are 5mm, 35mm, 95mm, and 155mm.
Let’s look at the 5mm height first. At 5mm off the ground, the flow is choked. Choked flow, in this case, is when the air velocity under the wing will not continue to increase no matter how much more the


Velocity at 5mm
Moving onto the 35mm height case, both velocity and coefficient of pressure plots look significantly better. The stagnation zone on the Coefficient of Pressure plot has decreased significantly.

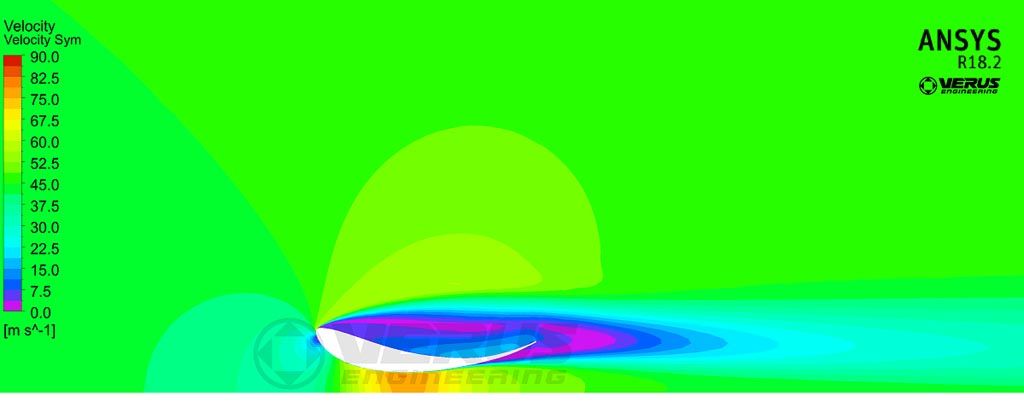
Velocity at 35mm
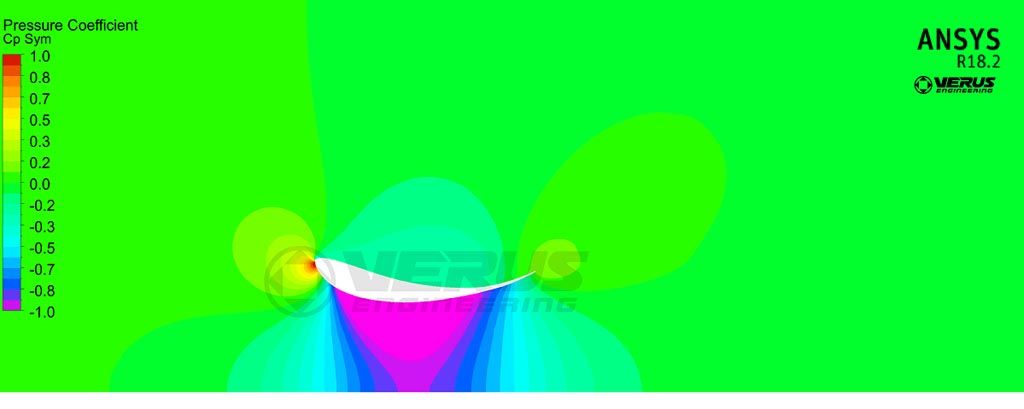
The next height we are viewing is 95 mm above the ground; which is the height the airfoil made maximum downforce. Just because maximum downforce was made at this height, does not mean maximum efficiency is at this height. Note the large low-pressure region under the wing shown in purple plus the decreased high-pressure region around the stagnation point.


Velocity at 95mm
The last height we will look into is 155mm height. The big item to notice at this height is the decrease of low pressure under the wing compared to the 95mm height. This decrease of the low-pressure zone is due to the wing reacting with the ground. When a wing is close enough to the ground, it makes a converging-diverging “duct” which increases the velocity on the bottom side of the wing, which results in more downforce production.

Velocity at 155mm
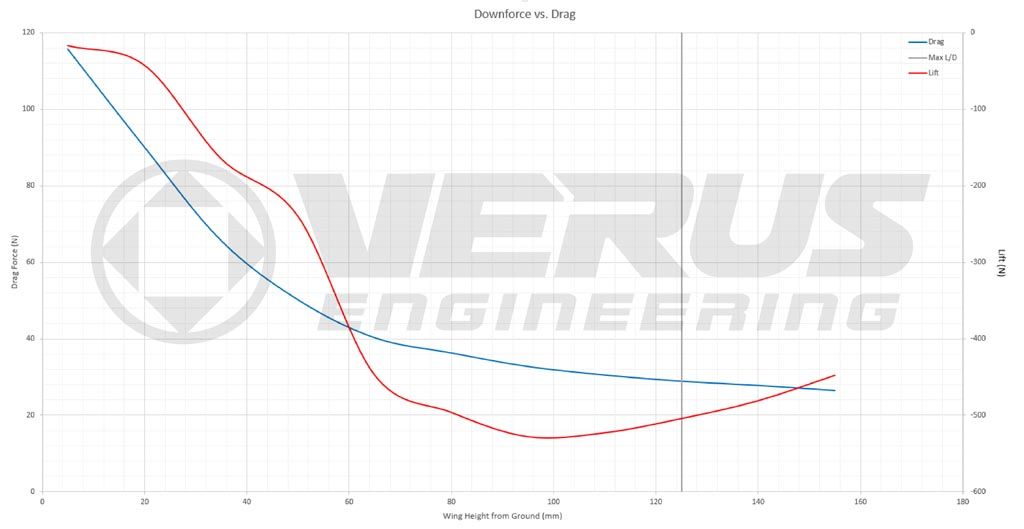
Downforce and Drag as it relates to wing height. Drag forces (N) is on the left while Lift forces are on the right y-axis. The x-axis is the height of the wing above the ground in mm.
Notice from the graph that downforce increases from 5mm all the way to 95mm; after that
All of these analyses were done at 45 m/s (100 mph). What would happen when velocity changes? Or with an object that is not a wing profile? Or a different AOA? Don't guess, analyze!
Location Matters, Why Guess?